Metaheuristics in large-scale global continues optimization: A survey

“Metaheuristics in large-scale global continues optimization:A survey” başlıklı çalışma Sedigheh Mahdavi, Mohammad Ebrahim Shiri ve Shahryar Rahnamayan tarafından yapılmış olup Information Sciences dergisinin 2015 yılındaki 295.sayının 407–428.sayfaları arasında basılmıştır.

Çalışmada 200’den fazla makale incelenerek metasezgisellerin büyük ölçekli küresel sürekli optimizasyon için getirdikleri çözümler üzerinde durulmuştur.

LSGO çözümü için önerilen yöntemlerin sınıflandırılması:

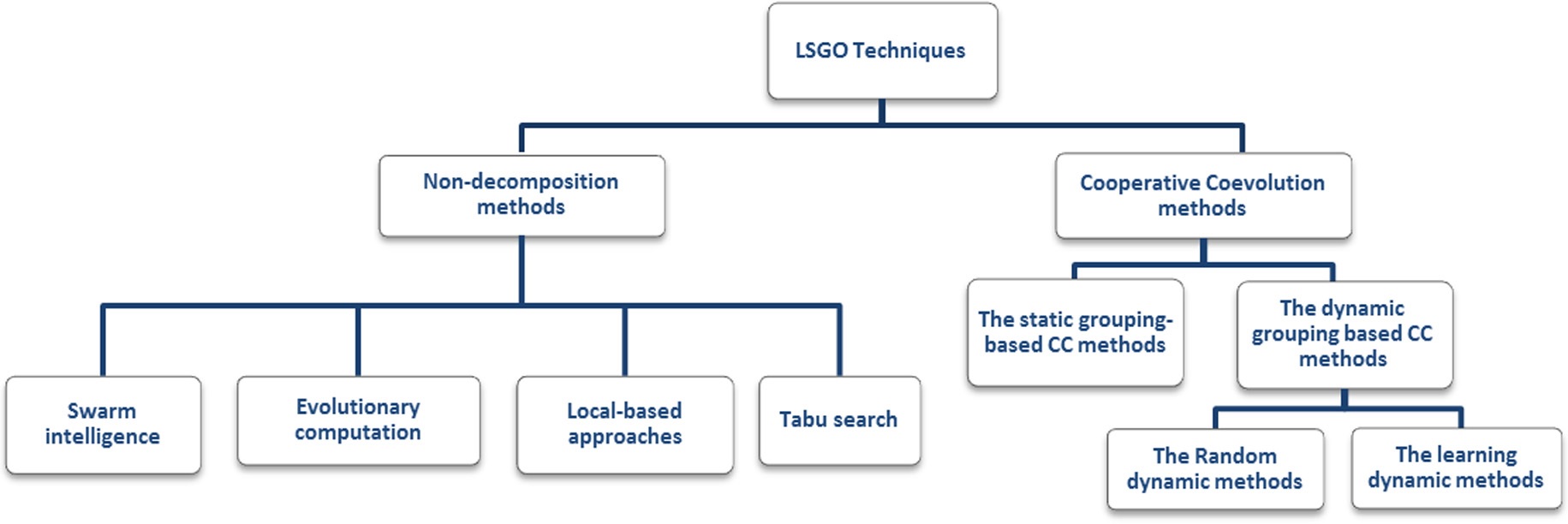
Cooperative Coevolution (CC) Birlikte Evrim algoritmaları problemi ayırma(decomposition) işlemi yaparak çözüme gitmeye çalışmaktadır. Bu yaklaşım böl ve fethet(divide-and-conquer) yaklaşımı temel alınarak geliştirilmiştir. Non-decomposition-based(Ayırma temelli olmayan) metodlar ise kullandıkları bazı efektif parametreler ile arama uzayını daha iyi araştırarak çözüm önerisi sunmaktadırlar.

Cooperative Coevolution (CC) Birlikte Evrim algoritmaları

İlk CC stratejileri tek boyuta indirgeme ve yarıya bölme şeklinde idi.

Cooperative Coevolution (CC) Birlikte Evrim süreci kabataslak aşağıdaki gibidir:

1.Adım: Büyük boyut daha küçük alt boyutlara bölünür
2.Adım: Round-robin(http://bilgisayarkavramlari.sadievrenseker.com/2008/11/19/round-robin/) stratejisi çerçevesinde önceden tanımlanmış iterasyon kadar alt bölümler işletirilir
3.Adım: n-boyutlu çözümü oluşturmak için tüm alt bileşenlerin çözümleri birleştirilir.

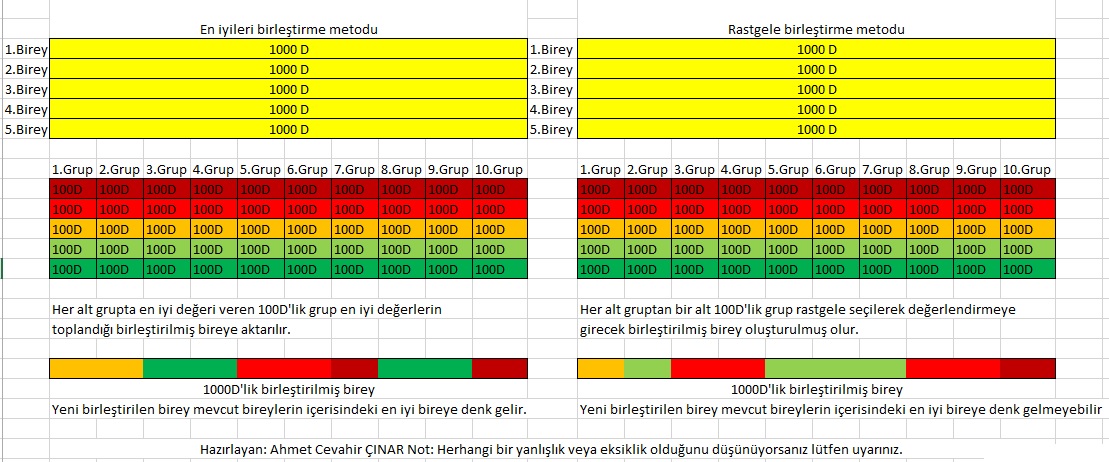
2 çeşit alt parçalardaki sonucu birleştirme metodu vardır.
1-Rastgele birleştirme metodu
2-En iyileri birleştirme metodu

2 çeşit ana gruplama stratejisi vardır.
1-Statik gruplama
2-Dinamik gruplama
2-a-Rastgele dinamik gruplama
2-b-Öğrenme temelli dinamik gruplama

Aşağıdaki tabloda farklı gruplama ve birleştirme stratejileri kullanarak yapılmış bazı çalışmalarla ilgili bilgilere yer verilmiştir:

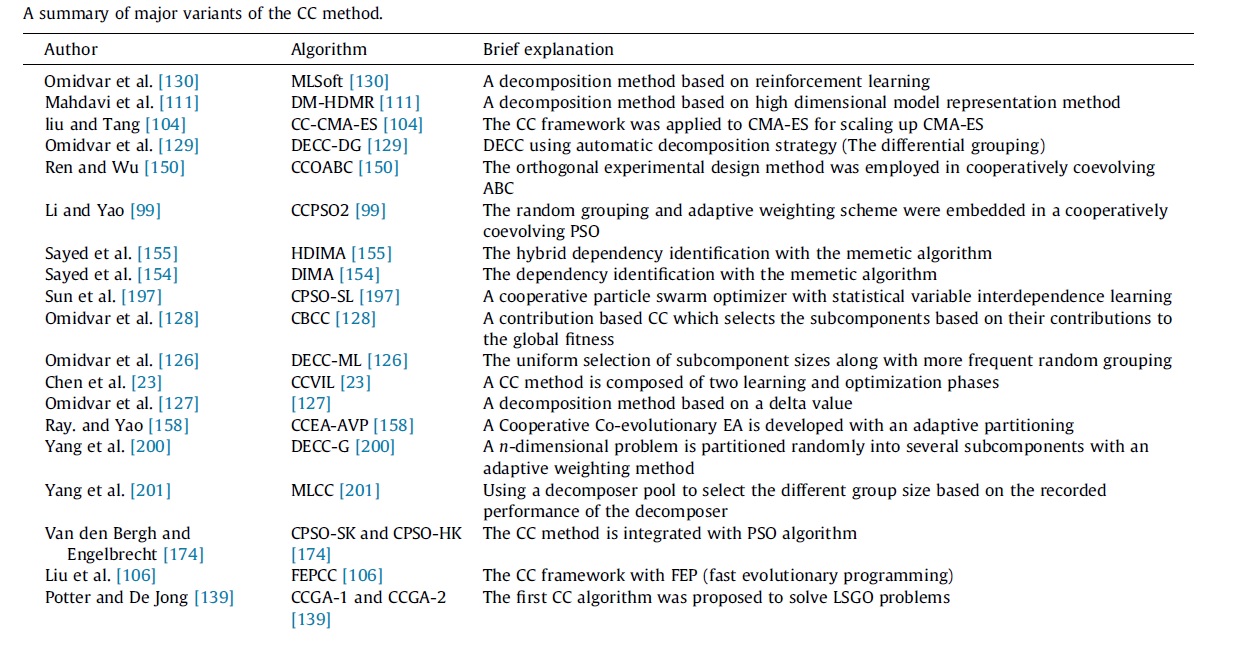
CC metodları ayrılabilir(separable) problemler için başarılı sonuçlar üretsede ayrılamayan(non-separable) problemlerde başarılı olamamışlardır. Bunun nedeni ayrılamayan problemlerdeki değişkenlerin birbirleriyle olan bağlantısıdır.

Statik gruplama

Statik gruplama önerisi ile yapılan çalışmalar genellikle 100 boyuttan daha düşük problemler için başarılı olurken, daha büyük boyutlarda çözüme ulaşamamışlardır. Ayrıca ayrılamayan(non-separable) problemlerde başarılı olamamışlardır.

Dinamik gruplama

Özellikle ayrılamayan(non-separable) problemlere çözüm olarak düşünülen bu yaklaşımda birbiri ile ilişkili parametrelerin aynı grupta toplanarak çözülmeleri sağlanmaya çalışılmıştır.

Dinamik gruplama, rastgele dinamik gruplama ve öğrenme temelli dinamik gruplama olarak ikiye ayrılabilir.

Rastgele dinamik gruplama

-Kooperatif birlikte evrim temelli rastgele dinamik gruplama ile çözüm önerisi:
1-n boyutlu vektör rastgele bir şekilde m adet s boyutlu vektöre bölünür. Örneğin 1000 boyutlu problem için 20 adet 50 boyutlu parça gibi.
2-Daha sonra her bir alt bölüm ilgili algoritma ile belirlenen FEs sayısı kadar adım çözülmeye çalışılır.
3-Her bir alt bölüme bir ağırlık vektörü atanır ve popülasyonun en iyi, en kötü ve rastgele çözümleri ile optimize edilmeye çalışılır.
4-Sonlandırma kriterine ulaşılmadıysa başa dönülür.

DECC-G algoritması ile rastgele gruplama metodu 1000 boyuta kadar olan ölçeklenebilir ayrılmaz(scalable non-separable) problemler için iyi sonuçlar üretmiştir, yalnız ilişkili parametreler arttıkça bu performans düşmüştür.

MLCC, JADE, CCPSO, CCPSO2, CCOABC algoritmaları da ilgili çalışmada kısa kısa anlatılmıştır.

Öğrenme temelli dinamik gruplama

Problemdeki ilişkili değişkenlerin hangileri olduğu uzman bilgisi gerektirmektedir. Bu bilgiyi optimizasyona başlamadan önce elde edebileceğimiz gibi, optimizasyon süresincede öğrenebiliriz. Öğrenme temelli dinamik gruplamanın amacı ilişkili değişkenleri aynı alt grup altına toplamaktır.

Hangi parametrelerin birbirleri ile ilişkili olduğunu bulmak için;

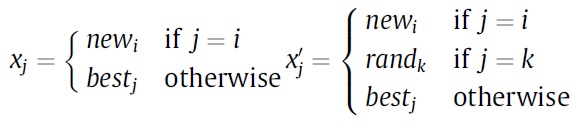
best= o ana kadar erişilmiş en iyi değer
new= mevcut çözüm
rand= rastgele çözüm

Üretilen 2 yeni çözüm(xj ve x’j) fonksiyon değerlemesine tutulur, eğer f(x’), f(x)’den daha iyiysek i ile k değişkenleri arasındaki etkileşim olasılığı(interaction probability) artırılır. k parametresi hesaba katıldığında çözüm iyileşiyorsa demek ki i ile k arasında bir ilişki vardır şeklinde bir yorum yapılabilir.

Chen ve ark. [Wenxiang Chen, Thomas Weise, Zhenyu Yang, Ke Tang, Large-scale global optimization using cooperative coevolution with variable interaction learning, in: Parallel Problem Solving from Nature, PPSN XI, Springer, 2010, pp. 300–309.] CC method with Variable Interaction Learning (CCVIL) isminde bir metod önermişlerdir.

[Mohammad Nabi Omidvar, Xiaodong Li, Xin Yao, Cooperative co-evolution with delta grouping for large scale non-separable function optimization, in: 2010 IEEE Congress on Evolutionary Computation (CEC), IEEE, 2010, pp. 1–8.] çalışmasında iki ardışık iterasyondaki boyutlar arasındaki değişimden elde edilen DELTA değerine göre gruplama yapılması düşünülmüştür. Birden fazla non-separable alt grup var ise performansı düşmektedir.

Önerilen bazı matematiksel teoremlere, varyanslara ve çeşitli istatistiki parametrelere bağlı ayırma stratejileri de geliştirilmiştir.

AYRIŞMAYAN YÖNTEMLER (Non-decomposition methods)

Ayrışmayan yöntemlerde böl ve fethet yaklaşımı yerine bölme yapmadan çözüme ulaşma yaklaşımı önerilmiştir. Bu yöntemlerde yeni mustasyon, seleksiyon, çaprazlama yöntemleri önerme, lokal arama dizaynı ve kullanımı, karşıtlığa dayalı öğrenme,örnekleme operatörü, Hibridizasyon, artan veya azaltılan popülasyon büyüklüğü yöntemleri öne çıkmaktadır.

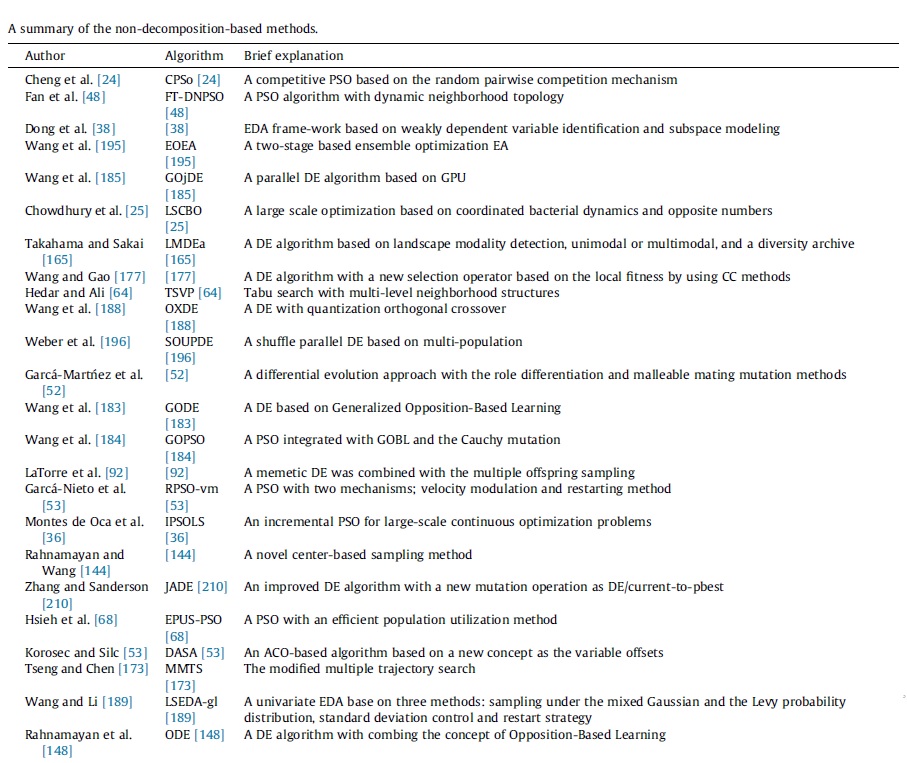
Sürü zekasına uygulanan ayrışmayan yöntemler

Popülasyonu etkin kullanmak için bireylerin popülasyondan çıkarılması veya eklenmesi hedeflenmiştir. Bunun için 3 kriter belirlenmiştir:

1-En iyi birey; k adet iterasyonda değiştirilmediğinde, sürüye yeni bir birey eklenir.
2-Bireyler, k adet iterasyonda en iyiyi en iyi duruma getirmek için bir veya daha fazla çözüm bulabilirse, arama ilerlemesini artırmak için gereksiz bireyler sürüden çıkarılır.
3-En iyi çözüm değiştirilmediğinde ve popülasyon büyüklüğü popülasyonun maksimum boyutuna eşit olduğunda, yeni bir birey eklemek için mevcut sürüdeki zayıf uygunluk değerine sahip bir birey çıkarılır.

-Bireylerin hareket alanını sınırlama,
-bireylerin standart sapma değerleri amaç fonksiyonunu çok küçük şekilde etkiliyorsa yeniden başlatma stratejisi,
-rotasyon matrisi ile bireylerin hareket alanına müdahale etme,
-her adımda bir çift birey seçerek bu iki bireyi yarıştırıp iyi olanı gelecek jenerasyona aktarırken, kötü olan bireyin ise iyi olana göre eğitilmesi,
gibi yaklaşımlar da önerilmiştir.

Durgunluğu engellemek(fighting stagnation) için ne yapılabilir? sorusuna “belirli bir durgunluk eşiğinden sonra yeniden başlatma(restarting) uygulanabilir” şeklinde bir cevap verilebilir.

Popülasyon çeşitliliğini artırmak için bir sonraki jenerasyona aktarılacak deneme bireyin seçimi yapılırken rastgele üretilen 0-1 aralığındaki bir sayı, önceden belirlenmiş (pr) değerinden küçükse mevcut bir sonraki jenerasyondaki birey, değilse mevcut jenerasyondaki birey deneme bireyine aktarılır. Aşağıda bu durumun gösterimi mevcuttur:

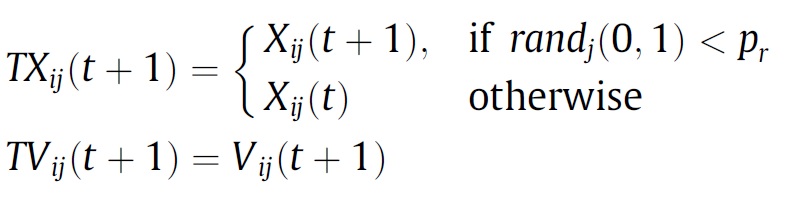
Evrimsel hesaplamaya uygulanan ayrışmayan yöntemler

Mutasyon operatörü uygulanırken bireylere açılar eklenmiştir. Bireyler bir matris formunda düşünülerek alt matrislere bölünerek işlem yapılması sağlanmıştır.

Bireylerin global korelasyon matrisi oluşturulur ve belirli bir eşik değerin altındaki değişkenler zayıf bağımlı değişkenler(weakly dependent variables) olarak adlandırılır.

Küresel daralma(global shrinking) olarak isimlendirilen teknikle arama uzayını potansiyel bölgeye çekmek için Gauss ve Cauchy modelleri kullanılır. Yerel keşif(local exploration) olarak isimlendirilen teknikle her grubun boyutu uyarlamalı olarak ayarlanır. Her alt grup farklı 3 algoritma ile çözümlenir ve fitness değerine en çok etki eden parametreler belirlenir.

Problemin unimodal mı multimodal mı olduğunu tespit etmek arama uzayına yapılacak davranışları etkilediğinden önemlidir.

Popülasyonun alt gruplara bölünerek her gruba bir ölçekleme faktörü verilmesi ve 0,1 ile 1,0 arasında rastgele değerleri alt gruplara ölçekleme faktörü olarak verme yaklaşımları da mevcuttur.

Cauchy mutasyon temelli global en iyi etrafında bir aday çözüm önerisi geliştirilmiştir.

Öklid uzaklık tabanlı çeşitlilik metriği(Euclidean distance-based diversity metric) temelli bir popülasyon çeşitliliği ölçüm metoduna göre fitness/çeşitlilik değerlerine bağlı yeni çözüm önerileri geliştirilmiştir.

Minimum Population Search (MPS) küçük popülasyon ile arama uzayını taramayı garanti etmektedir. MPS keşif ve sömürü dengesini iyi kurarak LSGO’ya çözüm bulmaya çalışmaktadır.

Karşıtlığa dayalı öğrenme ile bağlantılı yaklaşımlar

Popülasyon ilk oluşturulurken, bir de karşıt popülasyon oluşturulur ve iterasyonlar başlamadan bu iki popülasyon karşılaştırılarak en iyi olanlar tek popülasyon halinde bırakılır. Araştırma sürecinde de daha önceden belirlenen olasılık değerine göre her birey için oluşturulan karşıt birey ile işleme devam edilir.

Yerel arama ile bağlantılı yaklaşımlar

Quasi-Newton metodu ile yakınsama hızı artırılmaya çalışılmıştır. Yerel aramayı gerçekleştiren bir çok farklı yöntem önerilmiştir.

Tabu arama ile bağlantılı yaklaşımlar

Popülasyon daha alt parçalara bölünmüş, yerel arama gerçekleştirilmiş ve Tabu arama temelli bazı yaklaşımlar önerilmiştir.

Kıyas Fonksiyonları ve performans ölçümleri

CEC’08 setindeki
G1 (Shifted Sphere), G4 (Shifted Rastrigin),G6 (Shifted Ackley) : separable
G2 (Schwefel),G3(Shifted Rosenbrock),G5(Shifted Griewank),G7 (Fast Fractal):non-separable
olaran tanımlanmıştır.

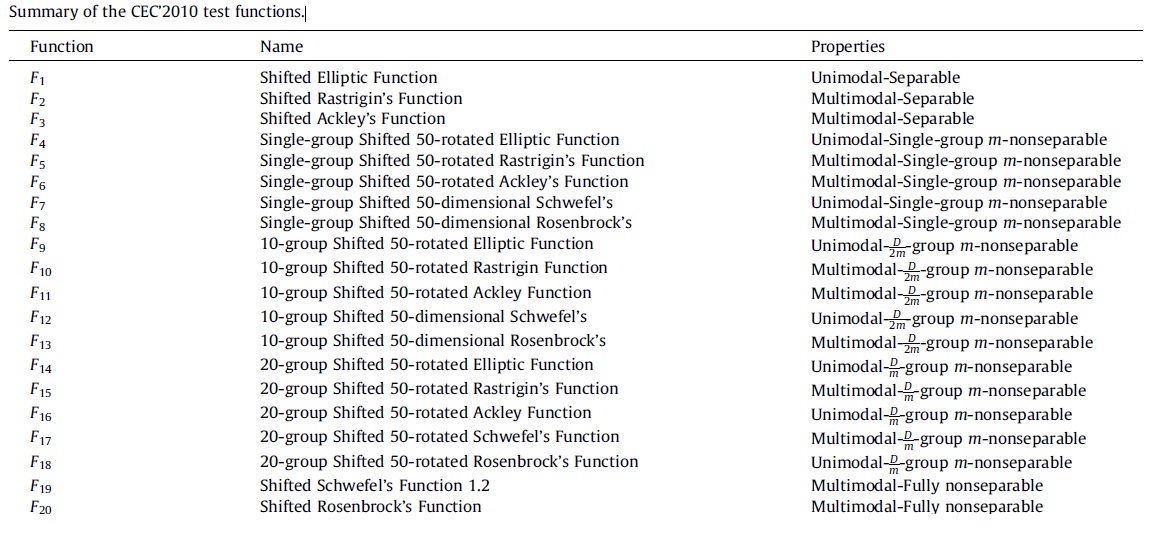
CEC’2010 test fonksiyonları:

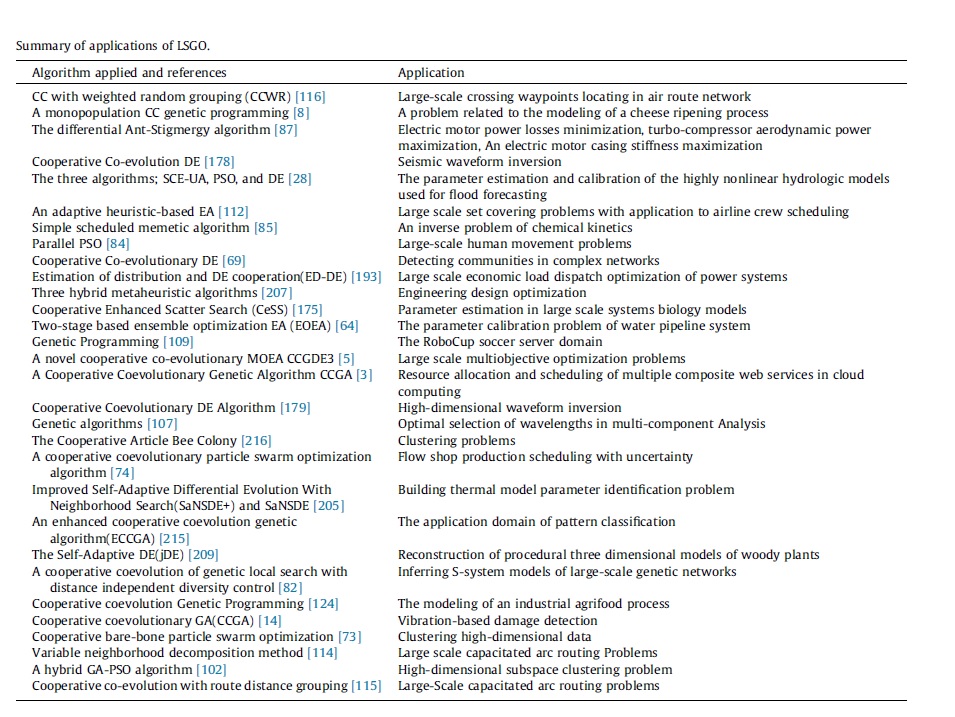
LSGO ile ilgili Örnek Uygulamalar:

Sonuç ve Değerlendirme

LSGO’nun çözümlemesinin zor olmasının sebepleri:

1-Boyut arttıkça arama uzayı büyümektedir
2-Boyut arttıkça problemin tipi değişebilir(unimodal -> multimodal)
3-Boyut arttıkça hesaplama maliyeti büyümektedir.
4-Non-seperable fonksiyonlar için ilişkili değişkenlerin tespit edilmesi.

Ne Yapılabilir?

1-Optimum bölümleme nasıl yapılabilir? İlişkili değişkenler nasıl tespit edilebilir?
2-CC algoritmaları kısmi çözümler üretmektedir, bu algoritmaların performansı nasıl artırılabilir?
3-Fully non-separable problemleri bölerek çözmek sonuç getirmediğinden ne gibi bir strateji ile çözülebilir? Bölümleme yapmadan çözüme ulaşmaya çalışan güçlü algoritmalar paralel olarak çalıştırılabilir. Bölümleme yapmadan çözüme ulaşmaya çalışan güçlü algoritmalar ile yerel arama tabanlı yaklaşımlar hibrit olarak kullanılabilir.
4-CEC’2013 kıyas fonksiyonları gerçek dünya problemlerini daha iyi karakterize etmektedir. Her geçen gün kıyas fonksiyonları güncellenmektedir. Güncellemeler yapıldıkça çözüm yöntemleri de başarısız olmaktadır bu yüzden sürekli çözüm önerileri geliştirilmektedir.
5-Gerçek dünya problemlerinden bazıları çözülmeli ve bunlardan bir kıyas fonksiyon seti oluşturulmalıdır.
6-1000 boyutun üzerindeki problemlerle pek ilgilenilmemektedir. Ölçeklenebilirlik çalışmaları yapılabilir.

Çalışmayı indirmek için:

metaheuristics-in-large-scale-global-continues-optimization-a-survey